Electrostatics#

  • Author:

  • Date:

  • Time spent on this assignment:

Note: You must answer things inside the answer tags as well as questions which have an A:.

Hide code cell content 
import numpy as np
import matplotlib.pyplot as plt
import math
#from jax.config import config
#config.update("jax_enable_x64", True)
#from jax import jit, grad
#import jax.numpy as jnp
#import jax

import matplotlib.animation as animation
from IPython.display import HTML
def resetMe(keepList=[]):
    ll=%who_ls
    keepList=keepList+['resetMe','np','plt','math','jax','jnp','jit','grad','HTML','animation','animateMe_singlePendula']
    for iiii in keepList:
        if iiii in ll:
            ll.remove(iiii)
    for iiii in ll:
        jjjj="^"+iiii+"$"
        %reset_selective -f {jjjj}
    ll=%who_ls
    plt.rcParams.update({"font.size": 14})
    return
resetMe()
import datetime;datetime.datetime.now()

datetime.datetime(2024, 9, 26, 5, 33, 21, 548206)

In this project we are going to explore electrostatic potentials.

Exercise 1. Electrostatics from static charges#

  • List of collaborators:

  • References you used in developing your code:

In this section we are going to start by exploring the electric field that is generated from distribution of point charges. In many cases, these will be distributions that you will be able to work with analytically and can verify in some limits.

Let us start by writing a function E(q,r,positions) where r is the location of the charge as a numpy array [x,y,z] and positions is a two-dimensional numpy array of size \(p \times 3\) which are the three-dimensional functions you want to report the position at. This function should return the electric field vectors at the \(p\) positions as a \(p \times 3\) numpy array.

Answer (start)
### answer here
Answer (end)

a. A Monopole#

Our goal now is to plot the electric field for various different charge distributions. We will start with a monopole - a single charge \(q\) - at the origin.

It’s a little bit difficult to plot the electric field in three-dimensions so instead are going to start by plotting the electric field in a two-dimensional slice.

Evaluate the field from a single negative charge of value -1 at the origin at \(z=0\) in a square \(-5 \leq x \leq 5\) and \(-5 \leq y \leq 5\). Let’s say we will do a resolution of 100x100 points.

An easy way to get the list that you need to input into your function is the following:

The code below generates a positions array that is \(100^2 \times 3\) which you can input to your function.

numPoints=100
xs=np.linspace(-5,5,numPoints)
ys=np.linspace(-5,5,numPoints)
X,Y=np.meshgrid(xs,ys)
Z=np.zeros((100,100))
positions=np.vstack((X.flatten(),Y.flatten(),Z.flatten())).T

Using your function, generate the electric field as output and plot it as below.

Plot the electric field

Once you have the electric field output, we can now plot it. We are only looking in the XY plane, so we are only going to plot the field lines which are in this plane ignoring field lines which are in the \(\hat{z}\) direction.

You can plot the field lines using

E_x=np.reshape(Field[0],(numPoints,numPoints))   
E_y=np.reshape(Field[1],(numPoints,numPoints))
E_z=np.reshape(Field[2],(numPoints,numPoints))

plt.streamplot(X,Y,E_x, E_y,  linewidth=1.0, cmap=plt.cm.inferno, density = 1.0, arrowstyle='->', arrowsize=1)
plt.colorbar()

It is sometimes interesting to also represent the total magnitude of the field lines (including the field in the z-direction) by including a color=Emag parameter to the streamplot.

Answer (start)
### answer here
Answer (end)

In addition to plotting the field lines, we would like to plot the electric field as a function of distance. We expect that this should decay as \(1/r^2\). Give your E function a set of positions which go from 0.1 to 4.0 in the x-direction (np.linspace) and are 0 in the y and z directions.

  • Make a plot of x versus the value of the field in the x-direction.

  • Also make a log-log plot. This should be linear.

  • Fit a line (np.polyfit(xx,yy,1)) to the log-log plot. You should get a slope of -2 which corresopnds to a decay of \(1/r^2\)

Answer (start)
### answer here
Answer (end)

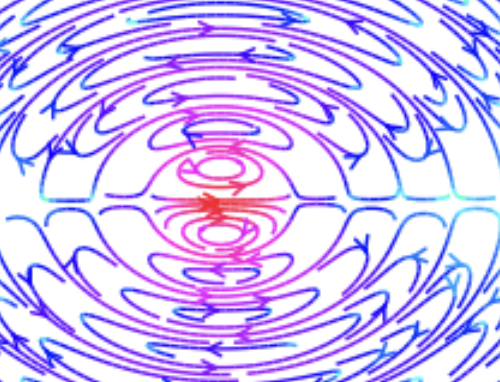
b. Dipole#

We essentially want to do the same thing as we did in part (a) but now with a dipole. A dipole consists of two oppositely valued charges which are located a distance \(d=2\) apart.

Plot the following:

  • Field lines for the dipole

  • \(E_x\) as a function of \(x\)

  • Show that at large \(x\), \(E_x \propto 1/x^3\). It’s important to be at large \(x\) here. I ploted from \(x=1.2\) to \(x=50\) and only fit the line after \(x=30\)

Answer (start)
### answer here

### answer here
Answer (end)

c. Quadrapole#

Now let’s do essentially the same thing with the quadropole where you have

  • two negative charges at (1,0,0) and (-1,0,0)

  • two positive charges at (0,1,0) and (0,-1,0)

Please plot the following

  • Field lines for the quadropole.

  • \(E_x\) as a function of \(x\)

  • Show that at large \(x\), \(E_x \propto 1/x^4\).

Answer (start)
### answer here
Answer (end)

d. Ring of Charge#

In this problem we are going to work on a ring of charge with radius \(a=1\) and total charge \(q=-1\) that is in the XY plane. In this problem you will

  • make a plot of the field lines in the

    • XY plane at z=0

    • XY plane at z=3

    • XZ plane at y=0

  • make a plot of the field at large \(x\). Show that at large \(x\), the ring of charge decays like \(1/r^2\), i.e. just like a single point. Explain why this is to be expected.

  • make a plot and show that at all \(z\) on the central axis of the ring that the electric field in the z direction goes as \(qz/(a^2+z^2)^{3/2}\)

Answer (start)
### answer here

### answer here

### answer here

### answer here

### answer here
Answer (end)

Exercise 2. Conductors#

In this exercise, our goal is to understand the role of point charges on conductors.