Classical Gates#
Extra Credit
Completing this page is worth 10 points extra credit
We’ve discussed a number of quantum gates and even described some subroutines which you can build out of quantum gates. But suppose instead we want to build a quantum circuit which implements a classical function - say some python function you’ve written.
Q: Why is this an interesting question?
Well, first we might want to know if a quantum computer is, at least, as powerful as a classical computer. Naively, you might think this is completely obvious but there is an important limitation to quantum computers which don’t exist for classical computers: quantum computers have to be reversible while classical computers don’t.
Secondly, suppose we have a classical python function \(f(x)\) which can take any number from \(0\) to \(2^{100}\). Classically, it would be impossible to run your function on all those numbers. If you had a set of quantum gates which was implementing \(f\) though, you could take \(\sum_i |i\rangle\) (generated by Hadamards on \(|0...0\rangle\)) and then generate \(\sum_i |f(i)\rangle\) which is a linear superposition over \(2^{100}\) function evaluations. Unfortunately, this state by itself isn’t useful. If we were to measure now we would just got a random value of \(f(x)\) (easy to get classically also by just running \(f\) on a random \(x\)). But, maybe there are some situations where we can post-process this state which has all \(2^{100}\) values of \(f\) in it and do something.
Reversible Classical Circuits#
In this section, we want to learn how to take a python function and generate a quantum circuit for it.
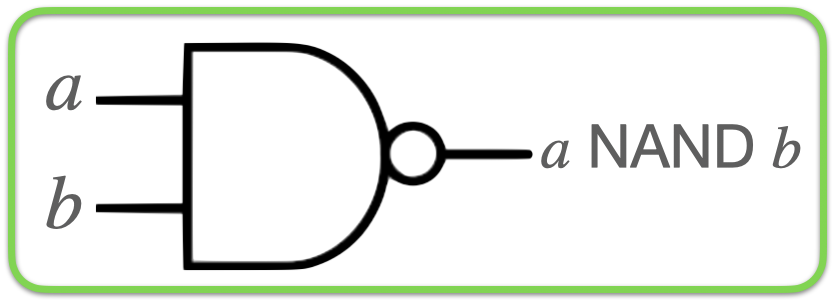
If I have a python function, the first thing I should do is convert it to a classical circuit. In particular, I want the circuit to only use nand gates. Any classical python function can be made out of nand gates because nand gates are universal. If the python function can run in time \(O(T)\) the number of NAND gates you need is going to be \(O(T \log T)\).
A nand gate (not-and) is a two bit gate which outputs 0 if the two inputs are 1. Otherwise it outputs 0 - i.e.
0 NAND 0: 1
0 NAND 1: 1
1 NAND 0: 1
1 NAND 1: 0
Unfortunately, nand gates aren’t reversible. If I told you the output of a nand-gate is 1, you don’t know whether the two inputs were 0,0 or 0,1 or 1,0. Consequently, a circuit made out of nand gates are also not going to be reversible.
To start fixing this problem, we are going to replace the nand gate with a gate that’s reversible. We are going to use a control-control-not (also called a toffeli gate). The control-not does nothing on the first two wires. The not happens on the third wire if the first two wires are 1 - i.e.
0 0 a: 0 0 a
0 1 a: 0 1 a
1 0 a: 1 0 a
1 1 a: 1 1 not a
Grading
The NAND gate has two inputs and one output. The toffeli has three inputs and three outputs. Choose two toffeli inputs and (either a \(|0\rangle\) or \(|1\rangle\) to map to (which order?) the three inputs of the toffeli so that one of the toffeli outputs is a NAND b.

Getting Reversibility#
Next we are going to do is replace each NAND gate with toffeli gates.
Grading
Write some code which takes a circuit of NAND gates and replaces them with toffeli. Apply this to a nor gate (you can look up how to generate this from NAND’s if it isn’t obvious to you. To emulate classical fan-out you may need to use the fact that a control-not classically copies bits).
Consider when we do this. We then get
where the \(|junk\rangle\) is the output of the extra two wires from each toffeli gate that isn’t the output of the NAND. Having the \(|junk\rangle\) there is actually a major problem because we can’t interference on the \(f(x)\) with the junk still there.
In some sense, we want \( |x\rangle \rightarrow |f(x)\rangle\). That’s not possible though because everything has to be reversible. Consider an adding circuit which takes
\(|2\rangle |3\rangle \rightarrow |5\rangle\) and \(|1\rangle |4\rangle \rightarrow |5\rangle\)
But then, what does the reverse circuit do:
\(|5\rangle \rightarrow |?\rangle|?\rangle\)
The most we could hope for is something like \(|2\rangle |3\rangle |0\rangle \rightarrow |2\rangle|3\rangle |5\rangle\) or more generically
We will get this (with some additional ancilla running around). Concretely, if we are using \(k\) NAND gates and \(f(x)\) is written on \(p\) bits and \(|x\rangle\) is written on \(b\) bits, we will end up with
\(|x\rangle |0^k\rangle |0^p\rangle \rightarrow |x\rangle |0^k\rangle |f(x)\rangle\).
There are an intermediate \(k\) wires that start and end 0 (and so can be re-used).
Removing the junk#
To pull this off, we need to figure out how to remove the extra junk that we naively would have.
At the moment, we have a unitary \(U\) which acts on \(b+k\) bits and gives \(U|x\rangle|0\rangle = |junk\rangle|f(x)\rangle\). Let’s figure out how to get rid of the junk.
The first step is to figure out how to get
Hint: Think about control-not gates.
The second step is to figure out how to get
Notice that to accomplish this we can essentially ignore the last register. The we really need to draw a circuit which takes
Hint: Think about what your original quantum circuit did (i.e. the quantum nor gate you have). Can you use that to get yourself this operation. This process is called uncomputing.
Grading
Put everything together. Write code that takes a circuit made out of NAND gates and then generates the equivalent classical version including removing all of the additional junk that is naively there.